Part 1 링크 :
Kaggle Ensembling Guide(mlwave) / 캐글 앙상블 가이드 한글 번역 / Part. 1
원글은 다음 링크의 글입니다. Kaggle Ensembling Guide | MLWave Model ensembling is a very powerful technique to increase accuracy on a variety of ML tasks. In this article I will share my ensembling..
jamm-notnull.tistory.com
이 글은 위 문서에 대한 자의적인 한글 번역본입니다. 번역을 하면서 이해한대로 설명을 더 추가할것이고, 아무리 시도해도 이해가 되지 않은 부분은 빠진 내용이 있을 수 있습니다. 영어 실력의 부족으로 번역이 매끄럽지 않을 수 있습니다. 댓글로 번역, 내용을 지적해주시면 감사한 마음으로 수정할 수 있도록 하겠습니다. 본문이 매우, 매우, 매우 긴 관계로 몇 편의 글로 끊어서 올릴 수 있습니다.
번역상 '나' 는 필자가 아니라, 원 글의 저자임을 밝힙니다.
스태킹 앙상블 & 블렌딩 (Stacked Generalization & Blending)
결과물들을 평균하는 방법은 아주 쉽고 괜찮은 방법이지만, 최고 순위의 캐글러들이 사용하는 유일한 방법은 아닙니다.
Netflix 대회
Netflix 측에서는 꽤나 인기를 끌었던 데이터 사이언스 대회를 주최했습니다. 참가자들은 영화를 추천해주는 추천 시스템을 만들어야 하는데, 참가자들은 그들의 결과물들을 앙상블하는 것을 예술의 경지까지 끌어올렸습니다. 넷플릭스는 결국 우승자의 솔루션을 도입하지 않기로 결정했는데, 그 이유는 '너무 복잡하기 때문' 이었습니다.
그럼에도 불구하고, 이 대회로 인해서 몇개의 논문들과 참신한 방법들이 나왔습니다.
- Feature-Weighted Linear Stacking
- Combining Predictions for Accurate Recommender Systems
- The BigChaos Solution to the Netflix Prize
상당히 흥미롭습니다. 당신의 '캐글 게임' 능력을 향상시키고 싶다면 읽어보면 좋은 글들입니다.
최종 결과물을 위해 수백 개의 예측모델들을 혼합(원 : blending) 하는 것은 참으로 인상깊습니다. 우리는 몇가지의 새로운 방법들을 오프라인으로 측정해 보았지만, 여기서 추가적으로 정확도를 올리는 것이 이것을 생산 환경에 적용하려는 엔지니어링에 관한 노력을 정당화하지는 못했습니다. - 넷플릭스 엔지니어들
(역주 : 여기서 정확도 몇 퍼센트 더 올리는걸 적용하는 것이 그렇게 의미 있을 정도로 효과적이지는 않았다 라는 의미 같습니다)
스태킹 (Stacked generalization)
스태킹 앙상블 (원 : Stacked generalization) 은 1992년 논문 에서 Wolpert 에 의해 처음 언급되었습니다. Breiman의 논문인 “Bagging Predictors“ 보다 2년 먼저 나왔네요. Wolpert 는 그의 또 다른 머신러닝 이론인 “탐색과 최적화에 공짜 점심은 없다“ 로도 유명합니다.
스태킹의 기본적인 아이디어는 여러 '기본 분류기' (원 : base classifiers) 들의 pool 을 사용한다는 것입니다. 그 후, 다른 분류기로 그 예측 결과를 조합하면서 일반화 오류를 낮추는 데에 목표를 두고 있습니다.
2-Fold Stacking 을 하는 예시를 들어보면 다음과 같습니다.
- train 데이터를 두 개 파트로 나눕니다 : train_a and train_b
- 1단계 모델은 train_a 를 학습해서 train_b 를 예측합니다.
- 같은 모델로 train_b 를 학습해서 train_a 를 예측합니다.
- 마지막으로 전체 train 데이터에 대해 학습한 후, test 셋을 예측합니다.
- 그리고 2단계 모델로 1단계 모델(들)의 예측 결과물을 학습합니다.
이 스태킹 모델은 문제 공간에 대해 1단계 모델의 예측값을 feature 로 추가적으로 받기 때문에, 단독으로 학습하는것보다 더 많은 정보를 가지고 학습을 하게 됩니다.
스태킹을 할 때, 0단계 모델들은 어느 하나의 변형이 아닌 가능한 한 모든 '타입' 들이어야 좋습니다. 이렇게 하면, 학습 데이터를 탐색하는 가능한 많은 방법들을 뽑아낼 수 있습니다. 이는 0단계 모델들은 '공간을 넓혀야 한다' 는 의미와 같습니다.
[…] 스태킹은 일반화 모델들을 비선형적으로 결합해서 새로운 일반화 모델을 만드는 것입니다. 각각의 모델들을 최적의 방법으로 통합하여 원래 모델이 학습 데이터에 대해서 예측해야했던 것들을 찾아야 합니다. 각각의 모델들이 뱉는 결과값이 다양할수록, 스태킹의 결과물은 더 좋아집니다 - Wolpert (1992) Stacked Generalization
블렌딩 (Blending)
블렌딩 (Blending) 이라는 말은 넷플릭스 우승자들이 처음 사용하였습니다. 이는 스태킹과 유사한 방법이지만, 비교적 더 단순하고 정보 누출의 위험이 적습니다. "Stacked ensembling" 과 "blending" 은 종종 같은 의미로 사용됩니다.
블렌딩을 사용할 경우, out-of-fold 예측값을 사용하는 대신에, 학습 데이터의 일부를 쪼개서 holdout validation 을 사용합니다. 다음 단계 모델은 이 holdout set 만을 이용해서 학습을 하게 됩니다.
블렌딩의 몇가지 장점은 다음과 같습니다.
- 스태킹보다 단순합니다.
- 0단계 모델과 이후 단계 모델이 다른 데이터를 사용하기 때문에 정보 누출에 더 강한 모습을 보입니다.
- 시드 값이나 Stratified Fold 를 팀원들과 공유할 필요가 없습니다. 누구나 모델을 만들고 'blender' 에 추가할 수 있고, 이 새로 추가한 모델을 사용할 것인가 폐기할 것인가에 대해서는 'blender' 가 결정할 뿐입니다.
몇가지 단점은 다음과 같습니다.
- 아무튼 사용하게 되는 데이터의 양이 적어집니다.
- 최종 모델이 holdout set에 대해 과적합 되었을 수 있습니다.
- Holdout set을 사용하는것 보다 교차 검증이 더 강인한 모습을 보여줍니다.
성능면에서는 스태킹과 블렌딩 두 기술 모두 비슷한 결과를 주지만, 어떤 것을 사용할 지는 당신의 선호에 따라 달라질 것입니다. 나같은 경우는 스태킹을 더 선호하는 편입니다. 만약 도저히 고르지 못하겠다면 둘 다 하는것도 방법입니다. 스태킹을 하고, 다음 단계 모델에서 holdout 셋을 사용해 블렌딩하는 것도 방법이 될 수 있습니다.
로지스틱 회귀분석 (Stacking with logistic regression)
로지스틱 회귀분석을 사용해서 스태킹을 하는 방법은 가장 기본적이고 전통적인 스태킹의 방법론입니다. Emanuele Olivetti 가 적었던 글 덕분에 나는 이것을 이해할 수 있었습니다.
test 세트에 대한 예측을 만들 때 한 번에 예측을 하거나 out-of-fold 예측값을 사용해서 평균을 구할 수도 있습니다. 사실 out-of-fold 로 평균을 구하는 것이 더 정확하고 깔끔한 방법이기는 하지만, 모델과 코딩의 복잡성을 낮추기 위해 나는 한번에 구하는 평균을 더 선호하는 편입니다.
캐글 예시 : “Papirusy z Edhellond”
나는 Emanuele 가 만든 blend.py 를 사용해서 이 대회에 나갔습니다. 8개듸 다른 모델들 (ExtraTrees, RandomForest, GBM...등등) 을 로지스틱 회귀분석으로 스태킹하는 방법은 0.99409 의 정확도를 내었고, 이 점수는 우승을 하기에 충분했습니다.
캐글 예시 : KDD-cup 2014
이 코드로 나는 Yan Xu의 모델을 더 향상시킬 수 있었습니다. 그녀의 모델은 스태킹 없이 0.605 정도의 AUC를 기록했지만, 스태킹을 하면서 0.625 정도로 향상되었습니다.
비선형 모델들의 스태킹 (Stacking with non-linear algorithms)
스태킹에 주로 사용되는 유명한 비선형 모델들은 GBM, KNN, NN, RF, ET 등등이 있습니다. 다중 분류 문제에서 원래의 feature 들을 비선형 스태킹 방법으로 결합하는것은 놀라울 정도의 성능 향상을 가져왔습니다. 분명히 첫 단계의 예측들은 가장 높은 순위의 'feature importance' 를 기록하고 있었고, 도움이 되는것을 확인할 수 있습니다. 비선형 알고리즘들은 원래의 feature 들과 meta-model의 변수들의 유용한 관계를 잘 찾아냅니다.
캐글 예시 : TUT Headpose Estimation Challenge
TUT Headpose Estimation 대회는 multiclass 분류 문제이면서 multi-label 분류 문제라고 볼 수 있습니다.
각각의 라벨 값에 대해서 다른 앙상블 모델을 학습시켰습니다. 다음 표는 각각의 모델의 결과물과, 각각의 클래스 확률을 ExtraTrees 로 스태킹하였을 때의 점수 향상을 보여줍니다.
MODEL | PUBLIC MAE | PRIVATE MAE
| Random Forests 500 estimators | 6.156 | 6.546 |
| Extremely Randomized Trees 500 estimators | 6.317 | 6.666 |
| KNN-Classifier with 5 neighbors | 6.828 | 7.460 |
| Logistic Regression | 6.694 | 6.949 |
| Stacking with Extremely Randomized Trees | 4.772 | 4.718 |
우리는 스태킹을 함으로써 각각의 모델의 결과보다 약 30%(! 씩이나) 좋은 결과를 얻을 수 있었습니다.
이 결과에 대해서는 다음 글을 읽어보시면 됩니다 : Computer Vision for Head Pose Estimation: Review of a Competition.
코드 예시
이 링크에서 out-of-fold 예측값을 만드는 함수를 찾을 수 있습니다. 결과물을 numpy 의 horizontal stack (hstack) 을 사용해서 blending 데이터셋을 만들면 됩니다.
Feature weighted linear stacking
Feature-weighted linear stacking 은 새로 만든 'meta-features' 들을 새로운 모델 예측으로 스태킹을 합니다. 이 새로운 스태킹 모델은 특정한 feature 값에 대해서 어떤 0단계 모델이 (원 : base predictior) 가장 좋은 모델인지를 학습할 것이라고 기대할 수 있습니다. 새로운 스태킹 모델(마지막 모델)로는 선형 알고리즘을 사용해서 마지막 모델의 결과가 관찰하기 단순하고 빠른 값을 낼 수 있게끔 합니다.
Vowpal Wabbit 으로 우리는 'feature-weighted linear stacking' 의 형태를 별도의 설치 없이 구현할 수 있습니다. 우리가 가진 학습 데이터가 다음과 같이 생겼다고 가정해봅시다.
1 | f f_1 : 0.55 f_2 : 0.78 f_3 : 7.9 | s RF : 0.95 ET : 0.97 GBM : 0.92
우리는 f-피쳐공간과 s-피쳐공간간에 -q fs(역주 : f 값 * s값 하나씩의 곱) 을 추가하면서 2차함수의 형태를 가진 변수간 상관관계를 추가할 수 있습니다.
f-피쳐공간의 이름들은 만들어진 'meta-features' 가 될 수도 있고, 원래의 'feature' 일 수도 있습니다. (역주 : 아무튼 f 는 스태킹 과정 상으로 s 보다 한단계 낮은 의미라는 뜻 같습니다.)
Quadratic linear stacking of models
이 이름은 이름 붙여진 것이 없어서 제가 새로 만들어낸 이름입니다. 'feature-weighted linear stacking' 과 상당히 유사하지만, 차이점은 모델들의 예측 결과들로부터 새로운 조합을 만들어낸다는 것입니다. 이것은 수많은 실험들 속에서 점수를 향상시켰고, Modeling Women’s Healthcare Decision competition 대회의 DrivenData 에서 특히 두드러졌습니다.
위에서 생각했었던 같은 예시를 다시 적어본다면 :
1 | f f_1 : 0.55 f_2 : 0.78 f_3 : 7.9 | s RF : 0.95 ET : 0.97 GBM : 0.92
우리는 2차원의 변수 상호작용인 -q ss 를 만들어서 학습을 시킬 수도 있습니다. (역주 : 예를 들면 : RF와 GBM의 예측값의 곱)
그리고 이 방법은 feature_weighted linear stacking (-q fs, -q ss) 와 쉽게 결합할 수 있고, 둘 다 성능 향상을 기대할 수 있을 것입니다.
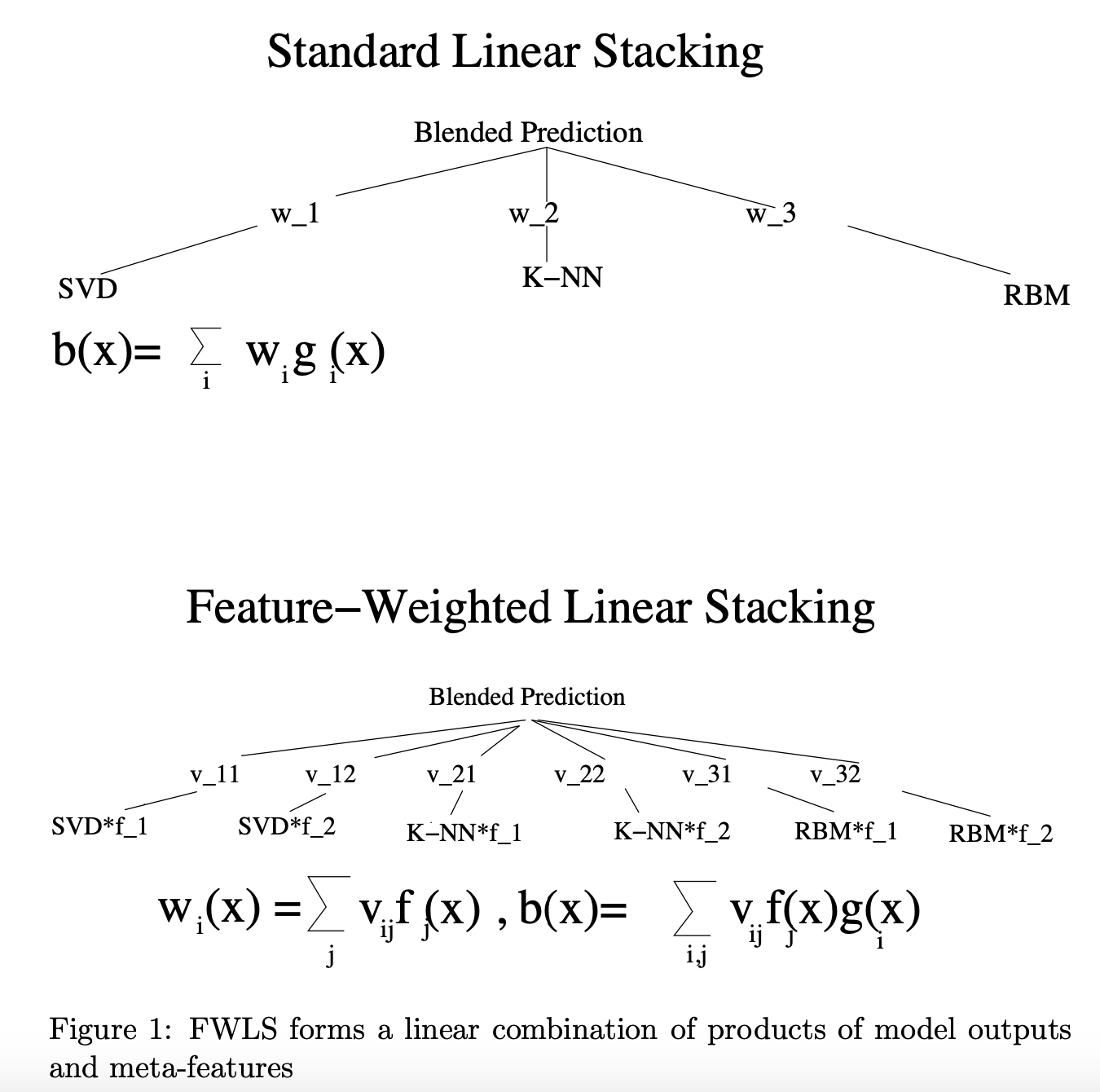
(역주 : 번역을 하긴 했지만 아직 예시를 찾아보지 않아서 이해가 잘 되지 않네요.
이미지 출처 -(Feature-Weighted Linear Stacking(2009) arxiv.org/pdf/0911.0460.pdf#page=3))
따라서 당신은 여러 가지 기본 모델들을 만들어야합니다. 실험을 하기 전에, 이중 어떤 모델이 마지막에 사용될 meta model 에 도움이 될 지 모릅니다. 2단계 스태킹 모델의 예시를 살펴본다면, base model 들은 약한 모델(원 : weak base model)이 선호되고 있습니다.
그런데 왜 이렇게 base model 들을 열심히 튜닝하는것입니까? 여기서 튜닝은 모델들의 다양성을 확보하는데 사용될 뿐입니다. 마지막 단계에서 어떤 모델이 유용할지는 모릅니다. 그리고 그 마지막 단계는 '선형' 단계가 될 가능성이 높습니다. 튜닝도 필요 없고, 약간의 sparsity 를 위한 파라미터 한 개 정도 가진 모델이지요. - Mike Kim, Tuning doesn’t matter. Why are you doing it?
Stacking classifiers with regressors and vice versa
(역주 : Regressor 들을 모아서 마지막에만 Classification을 사용한다던가, 혹은 그 반대의 경우)
스태킹을 한다면, 당신은 Regression 문제에도 Classifier들을 사용할 수 있고, 그 반대도 가능합니다. 예를 들면 이진 분류 문제에서 base ㅡmodel 로 quantile regression 을 사용할 수 있습니다. 좋은 스태킹 모델은 Regression모델들이 최고의 분류 성능을 주지 않더라도 그 예측값으로부터 정보를 뽑아낼 수 있어야 합니다.
하지만 반대로 Regression 문제에서 Classifier 들을 사용하는것은 약간 더 까다롭습니다. 그래서 첫 번째 단계가 'binning' 이라고 하는 방법인데, 정답값(원 : y-label) 에 binning 을 균등한 간격으로 해주면, Regression 문제는 다음과 같이 다중 분류 문제로 바뀌게 됩니다.
- 20000 미만 : class 1.
- 20000 이상, 40000 미만 : class 2.
- 40000 이상 : class 3.
각각의 클래스에 대한 확률을 구한다면 (마지막에 사용할) 스태킹 회귀 모델이 예측을 더 잘 할 수 있도록 도와줄 것입니다.
“나는 절대, 절대로 out-of-fold 예측값 없이는 어디도 가지 않을거라고 배웠습니다. 내가 하와이를 가던, 어디 화장실을 가도 난 이 예측값들을 가져갈 겁니다. 내가 언제 2단계 혹은 3단계 'meta classifier' 들을 학습시켜야 할지 모릅니다. ” - T. Sharf
비지도학습으로 만든 feature 들의 스태킹 (Stacking unsupervised learned features)
우리가 꼭 스태킹을 할때 지도학습만을 사용해야한다는 규정은 그 어디에도 없습니다. 당연히 비지도학습 방법들도 사용할 수 있습니다.
K-Means 클러스터링은 여기서 사용될 수 있는 인기있는 좋은 방법 중 하나입니다. Sofia-ML 에서는 여기에 적합한 빠른 K-Means 알고리즘을 구현해두었습니다.
최근에 있었던 다른 방법 중 하나는 t-SNE를 사용하는 것입니다. 데이터를 2차원 혹은 3차원으로 축소시킨 후 이 결과물들을 비선형 스태킹 모델로 학습시키는 것입니다. 이 경우에는 holdout set을 확보해 두는것이 스태킹, 블렌딩 모두에서 안전한 방법일 것 같습니다. 여기서 Mike Kim이 t-SNE 벡터들을 XGBoost 로 부스팅한 솔루션을 볼 수 있습니다. ‘0.41599 via t-SNE meta-bagging‘.
Piotr 에서 Otto Product Classification Challenge 데이터를 t-SNE 로 시각화한 좋은 결과를 볼 수 있습니다.
Online Stacking
나는 online stacking 의 아이디어를 생각해내기 위해 꽤 많은 시간을 보냈습니다. 첫번째로, 해시된 이진 표현으로부터 아주 작은 임의의 tree 기반 모델을 만들었습니다. 거기에 이 모델이 정확한 예측을 한 경우 이득(원 : profit) 을 더해주고, 틀린 경우에는 빼주었습니다. 그 후, 가장 좋은 트리와 (원 : most profitable) 가장 안좋은 트리(원 : least profitable)를 가져와서 변수 (원 : feature representation) 에 더해주었습니다.
이 방법이 먹히기는 했는데 인공적인 데이터에서 만 먹혔습니다. 예를 들면, 이런 방식으로 만든 랜덤한 트리모델들을 선형 퍼셉트론으로 학습시켜도 비선형 문제인 XOR 문제를 학습하는데 성공했습니다. 하지만 다른 실생활 문제들에는 전혀 먹히지 않았습니다. 믿어주세요. 진짜 해봤는데 안돼요. 이 이후로 나는 새로운 알고리즘을 소개하는 논문을 볼 때 인공적인 데이터들로만 실험한 것을 보면 의심을 하기 시작했습니다.
하지만 이와 유사한 아이디어가 이 논문 (random bit regression)에서 성공했습니다. 여기서 보면, 여러 feature 들로부터 생성한 임의의 선형 함수를 여러 개 만들었고, 가장 좋은 것은 강한 정규화를 통해 찾아졌습니다. 여기서 나는 다른 데이터셋에서도 적용될 수 있는 성공적인 방법을 찾을 수 있었습니다. 이는 다음에 쓸 포스트 내용이 될 것입니다.
이 online stacking 의 예시로는 광고 클릭 여부 예측 문제를 들 수 있습니다. 각 모델들은 그때그때 잘 작동되는 최근의 데이터로 학습됩니다. 따라서 데이터가 시간적인 관계가 있으면, Vowpal Wabbit 을 사용해서 전체 데이터를 학습시키고, 더 복잡하고 강력한 XGBoost 같은 툴을 사용해서 과거의 데이터를 학습시키는 방법을 사용할 수 있습니다. 이렇게 학습된 XGBoost 모델들의 예측값과 원래의 샘플들을 같이 스태킹하면, Vowpal Wabbit이 가장 잘 하는것을 제대로 시킬 수 있습니다. 손실 함수 최적화 말이지요.
실제 세계는 복잡합니다. 그래서 서로 다른 모델을 많이 결합하면 이러한 복잡성을 포착할 수 있습니다. - Ben Hamner ‘Machine learning best practices we’ve learned from hundreds of competitions’ (video)
Everything is a hyper-parameter
스태킹, 블렌딩, 메타모델링을 할 때, 내가 하는 모든 행동들이 스태킹 모델에게는 일종의 하이퍼파라미터로 적용될 수 있다고 생각해야 합니다. 예를 들면:
- 데이터를 스케일링하지 않는것.
- 데이터를 Standard Scaling 하는것.
- 데이터를 Minmax Scaling 하는 것.
이 모든 것들은 앙상블 학습의 성능을 끌어올리기 위해 튜닝해야하는 추가적인 하이퍼파라미터일 뿐입니다. 마찬가지로, 사용할 base model 의 수 역시도 최적화해야할 하이퍼파라미터로 볼 수도 있습니다. Feature selection 이나 결측치 처리 역시도 다른 예시가 될 수 있습니다.
이러한 'meta-parameter' 들을 튜닝하는데는 평소 알고리즘 튜닝에 사용하는 random search 나 gridsearch가 좋은 방법이 될 수 있습니다. Li
가끔씩은 XGBoost 가 KNN-Classifier 가 보는 것들을 보게 해주는것이 효과적일 때도 있다 . – Marios Michailidis
Model Selection
여기서 추가적으로 여러가지 앙상블 모델들의 결과를 조합해보면서 점수를 더 최적화할 수 있습니다.
- 접근 방법은 수동으로 선택한 좋은 앙상블 결과들에 평균내기, 투표 방식, 순위 평균을 구해 보는 것입니다.
- 탐욕 알고리즘적인 방법 (원 : Greedy forward model selection (Caruana et al.)) - 3개 정도의 가장 좋은 모델을 시작으로, train set의 점수를 가장 많이 올려주는 다른 모델들을 하나씩 추가합니다. 복원 추출 개념을 적용하면, 한 개의 모델이 여러번 선택되어 추가될 수 있고, 이것은 가중치를 부여하는 효과가 있습니다. (원 : weighing)
- 유전 알고리즘적인 방법 - 유전 알고리즘과 교차 검증 점수를 사용해서 선택할 모델들을 정합니다. 예시로 inversion의 솔루션을 볼 수 있습니다. ‘Strategy for top 25 position‘.
- 나는 Caruana 의 방법에서 아이디어를 얻은 완전히 랜덤한 방법을 사용합니다. 먼저 랜덤한 앙상블 결과를 100개 정도 만들고, 비복원추출로 고른 몇 개의 결과를 골라내고, 이 결과 중 가장 좋은 결과를 고릅니다.
자동화 (Automation)
Otto product classification 대회를 하면서 스태킹을 진행할 때, 나는 top 10 등의 자리에 빠르게 올라갔습니다. 거기에 더 많은 기본 모델들을 추가하고, 스태킹 앙상블들을 bagging 했다면 점수를 더 향상시켰을 수 있을겁니다.
7개의 base model 들을 6개의 스태킹 모델로 스태킹하는 정도가 되었을때, 나는 충격과 공포를 느꼈습니다. 이 모든 과정을 자동화할 수는 없을까? 이 복잡하고 느리면서 다루기 힘든 모델들을 계속 만지는 것은 내가 좋아하는 '빠르고 단순한' 기계 학습의 영역에서 완전히 벗어나있는 일이었습니다.
나는 대회의 남은 기간동안 이 스태킹 과정을 자동화 시키는 일에 시간을 쏟았습니다. 기본 모델로는 랜덤한 알고리즘들을 랜덤한 파라미터들로 학습을 시켰습니다. Scikit-learn의 API 를 가지는 Wrapper 들을 VW, Sofia-ML, RGF, MLP and XGBoost 등과 함께 사용했습니다.
The first whiteboard sketch for a parallelized automated stacker with 3 buckets
스태킹 모델로는 SVM, Random Forests, ExtraTrees, GBM, XGBoost 들을 랜덤한 파라미터로, 기본 모델들의 랜덤한 집합에 학습을 시켰습니다. 마지막으로, 이 스태킹 모델들은 각각의 fold-prediction 이 더 낮은 점수를 갱신할 때 그 값을 평균내었습니다.
이렇게 자동으로 만들어진 스태킹 모델은, 대회 마감 약 일주일 전에 57등을 기록하고 있었습니다. 이는 나의 최종 앙상블 모델에 기여하게 되었습니다. 기존에 내가 하던 방법과 다른 점이라고는 모델을 튜닝하고, 고르는 것에 전혀 시간을 쓰지 않았다는 점입니다. 코드를 실행하고, 자고 일어나면 점수가 올라 있죠.
이렇게 만들어진 자동 스태킹 모델은 아무 튜닝이나 모델 선택을 하지 않고도, 3000여 명의 경쟁자들 중에서 상위 10%의 성적을 거두었습니다.
이러한 자동화된 스태킹 모델은 내 가장 큰 관심 분야중 하나입니다. 여기에 관한 다음 몇 개의 글들도 기대해주세요. 이 자동 스태킹 모델은 TUT Headpose Estimation challenge 에서 가장 좋은 결과를 보여주었습니다. 이 'black-box' 솔루션이, 요즘 잘나가는 전문가들이 이 대회를 위해서 만든 특수 목적 알고리즘을 만든 것들을 모두 부숴버렸습니다.
주목할 만한 점은 : 이 대회는 다중 분류 문제입니다. 예측값들은 "yaw", "pitch" 두 가지를 모두 맞춰야합니다. (역주 : 한글로는 롤, 피치, 요 라고 하는데, 물체의 회전움직임, 혹은 방향을 3개 축으로 표현하는 방법이다 라고 보시면 됩니다.)
머리의 자세를 표현하려면, 이 "yaw" 와 "pitch" 들은 서로 관계가 있습니다. "yaw" 를 집중적으로 맞추는 모델들을 스태킹하는것이 "pitch" 값의 정확도도 올려주었고, 그 반대도 마찬가지였습니다. 흥미롭네요.
CV 점수를 고려할 때, 이 CV 점수들의 표준편차도 고려할 수 있습니다. 아무래도 표준편차가 작은 모델이 더 안전한 모델입니다. 이 다음에는 모델의 복잡도와 메모리 사용량, 그리고 코드 실행 시간을 최적화할 수 있습니다. 마지막으로는 각 예측 결과물들에 대한 상관관계를 추가해볼 수 있습니다. 코드가 자동으로 앙상블을 수행할 때, 상관관계가 적은 예측값들을 자동으로 선호할 수 있도록 말이지요.
이 자동화된 스태킹 파이프라인은 병렬화 및 분산화가 가능합니다. 그렇게 되면, 단일 노트북 컴퓨터로 실행해도 빠른 속도와 성능 향상을 기대할 수 있습니다.
Contextual bandit optimization 은 gridsearch 를 대신할 수 있는 방법입니다. 알고리즘이 좋은 파라미터와 모델을 사용하기 시작하고, 전에 사용했던 SVM 이 메모리가 부족했던 경우 등등을 기억하기를 원합니다. 스태킹에 관한 이 추가 사항은 다음에 더 자세히 살펴보겠습니다.
그 동안, MLWave 의 깃헙 저장소의 미리보기를 한번 보세요. “Hodor-autoML“.
Otto Product Classification Challenge 의 1등, 2등 수상자들은 1000개 이상의 다른 모델들의 앙상블을 수행했습니다. 솔루션은 여기에서 확인할 수 있습니다. 1위 솔루션, 2위 솔루션
Why create these Frankenstein ensembles?
(역주 : 이런 괴물같은 앙상블을 왜 하는 것일까요?)
이렇게 천 개가 넘는 모델들을 만들고 스태킹하고 조합하는 것이 당신이 보기에는 무익하고, 미친 소리처럼 들릴 지 모릅니다. 하지만 이런 괴물같은 앙상블들은 다 쓸모가 있습니다. :
- 캐글같은 대회를 우승할 수 있습니다.
- 한번의 시도로 잘나가는 최신 벤치마크들을 이길 수 있습니다.
- 모델을 만든 후, 이 좋은 성적과 단순하고 만들기 쉬운 모델의 성적을 비교해볼 수 있습니다.
- 언젠가 지금 수준의 컴퓨터들과 클라우드 컴퓨팅 자원은 아주 약한 날이 올 것입니다. 그 때에 대비해서 준비할 수 있습니다
- 이렇게 앙상블한 모델에서 얻은 지식을 다시 단순하고 얕은 모델에게 전달할 수 있습니다. (Hinton’s Dark Knowledge, Caruana’s Model Compression)
- 모든 기본 모델들이 제 시간안에 학습이 끝나지 않아도 됩니다. 한 개의 모델이 없어도, 앙상블 모델은 좋은 예측값을 만드는 데에 큰 지장이 없습니다. 그런 점에서 앙상블은 아주 graceful 한 degradation(역주 : 도저히 어떻게 번역해야 할지 모르겠습니다.) 의 형태를 소개합니다.
- 자동화된 대규모 앙상블은 어떠한 튜닝이나 모델 선택을 하지 않아도 오버피팅에 강력하고, 정규화(regularization)의 성질이 있습니다. 일반인들도 충분히 사용할 수 있습니다.
- 현재까지 머신러닝 알고리즘의 성능을 향상시키는 가장 좋은 방법입니다. 아마도 human ensemble learning에 관해서 무언가를 알려줄 수도 있습니다.
- 정확도를 1% 정도 올리는 것이 돈을 투자하는 일에 있어서는 큰 손실을 볼 것을 줄여주기도 할 것입니다. 더 심각한 예시로, 헬스케어 관련해서는 목숨을 살리는 일에 도움을 줄 수도 있습니다.
Update: Thanks a lot to Dat Le for documenting and refactoring the code accompanying this article. Thanks to Armando Segnini for adding weighted averaging. Thanks a lot everyone for the encouraging comments. My apologies if I have forgotten to link to your previous inspirational work. Further reading at “More is always better – The power of Simple Ensembles” by Carter Sibley, “Tradeshift Benchmark Tutorial with two-stage SKLearn models” by Dmitry Dryomov, “Stacking, Blending and Stacked Generalization” by Eric Chio, Ensemble Learning: The wisdom of the crowds (of machines)by Lior Rokach, and “Deep Support Vector Machines” by Marco Wiering.
Terminology: When I say ensembling I mean ‘model averaging’: combining multiple models. Algorithms like Random Forests use ensembling techniques like bagging internally. For this article we are not interested in that.
The intro image came from WikiMedia Commons and is in the public domain, courtesy of Jesse Merz.
Cite
If you use significant portions or methods from this article in a scientific paper, report, or book, please consider attributing with:
- Hendrik Jacob van Veen, Le Nguyen The Dat, Armando Segnini. 2015. Kaggle Ensembling Guide. [accessed 2018 Feb 6]. https://mlwave.com/kaggle-ensembling-guide/
or, if you prefer a more authoritative reference:
- Michailidis, Marios. (2017). Investigating machine learning methods in recommender systems (Thesis). University College London.
For other, less formal, material, such as blogs or educational slides, a simple link will suffice to satisfy Creative Commons 3.0 attribution.
The resource URL will remain static and the page hosted on this site for the foreseeable future.





























